Logaritma
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Grafik logaritma terhadap basis yang berbeda. merah adalah terhadap basis e, hijau adalah terhadap basis 10, dan ungu adalah terhadap basis 1.7. Perhatikan bahwa grafik logaritma terhadap basis yang berbeda selalu melewati titik (1,0)
Rumus dasar logaritma:

Pada rumus ini, a adalah basis atau pokok dari logaritma tersebut.
Beberapa buku dan karya ilmiah menuliskan
 sebagai
sebagai  . Notasi yang kedua umumnya ditemukan pada buku dan karya ilmiah yang berbahasa inggris.
. Notasi yang kedua umumnya ditemukan pada buku dan karya ilmiah yang berbahasa inggris.Basis
Logaritma yang paling umum digunakan adalah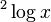 ,
,  atau
atau 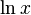 , dan
, dan  . Fungsi-fungsi tersebut memiliki basis 2, e, dan 10.
Logaritma dengan basis e juga disebut 'logaritma natural', dimana:
. Fungsi-fungsi tersebut memiliki basis 2, e, dan 10.
Logaritma dengan basis e juga disebut 'logaritma natural', dimana:

Notasi
- Di Indonesia, kebanyakan buku pelajaran Matematika menggunakan notasi blog a daripada logba. Buku-buku Matematika berbahasa Inggris menggunakan notasi logba
- Beberapa orang menulis ln a sebagai ganti elog a, log a sebagai ganti 10log a dan ld a sebagai ganti 2log a.
- Pada kebanyakan kalkulator, LOG menunjuk kepada logaritma berbasis 10 dan LN menunjuk kepada logaritma berbasis e.
- Pada beberapa bahasa pemrograman komputer seperti C,C++,Java dan BASIC, LOG menunjuk kepada logaritma berbasis e.
- Terkadang Log x (huruf besar L) menunjuk kepada 10log x dan log x (huruf kecil L) menunjuk kepada elog x.
Mencari nilai logaritma
Cara untuk mencari nilai logaritma antara lain dengan menggunakan:- Tabel
- Kalkulator (yang sudah dilengkapi fitur log)
Rumus
| ac = b → ª log b = c | ||
|---|---|---|
| a = basis | ||
| b = bilangan yang dilogaritma | ||
| c = hasil logaritma | ||
| Sifat-sifat Logaritma | ||
| ª log a = 1 | ||
| ª log 1 = 0 | ||
| ª log aⁿ = n | ||
| ª log bⁿ = n • ª log b | ||
| ª log b • c = ª log b + ª log c | ||
| ª log b/c = ª log b – ª log c | ||
| ªˆⁿ log b m = m/n • ª log b | ||
| ª log b = 1 ÷ b log a | ||
| ª log b • b log c • c log d = ª log d | ||
| ª log b = c log b ÷ c log a | ||

0 komentar:
Posting Komentar